Βέλτιστος σχεδιασμός αγωγών μεταφοράς πετρελαίου

Το Εθνικό Κέντρο Έρευνας Φυσικών Επιστημών “Δημόκριτος”, συνεχίζοντας μία μακρά παράδοση, διοργάνωσε από 4 έως 15 Ιουλίου 2016 Θερινό Σχολείο προσανατολισμού και ενημέρωσης, που απευθύνεται σε πτυχιούχους και τελειόφοιτους ΑΕΙ/ΤΕΙ.

Οι διαλέξεις του Θερινού Σχολείου καλύπτουν τις παρακάτω θεματικές περιοχές:

• Περιβάλλον – Ενέργεια – Ασφάλεια
• Προηγμένα Υλικά, Μικρο – Νανοτεχνολογία & Διατάξεις
• Βασική Έρευνα στις Φυσικές Επιστήμες
• Τεχνολογίες Πληροφορικής και Τηλεπικοινωνιών
• Επιστήμες Ζωής
• Νέες Τεχνολογίες και Πολιτιστική Κληρονομιά.

Οι διαλέξεις του Θερινού Σχολείου πραγματοποιήθηκαν από διακεκριμένους επιστήμονες από Ερευνητικά Κέντρα και Πανεπιστήμια της Ελλάδας και του εξωτερικού  και του ΕΚΕΦΕ ''Δ''. Επίσης στο πλαίσιο του Θ.Σ. πραγματοποιήθηκαν επισκέψεις στις εργαστηριακές εγκαταστάσεις του κέντρου και πρακτική εξάσκηση σε επιλεγμένα εργαστήρια.

Περίληψη της ομιλίας:

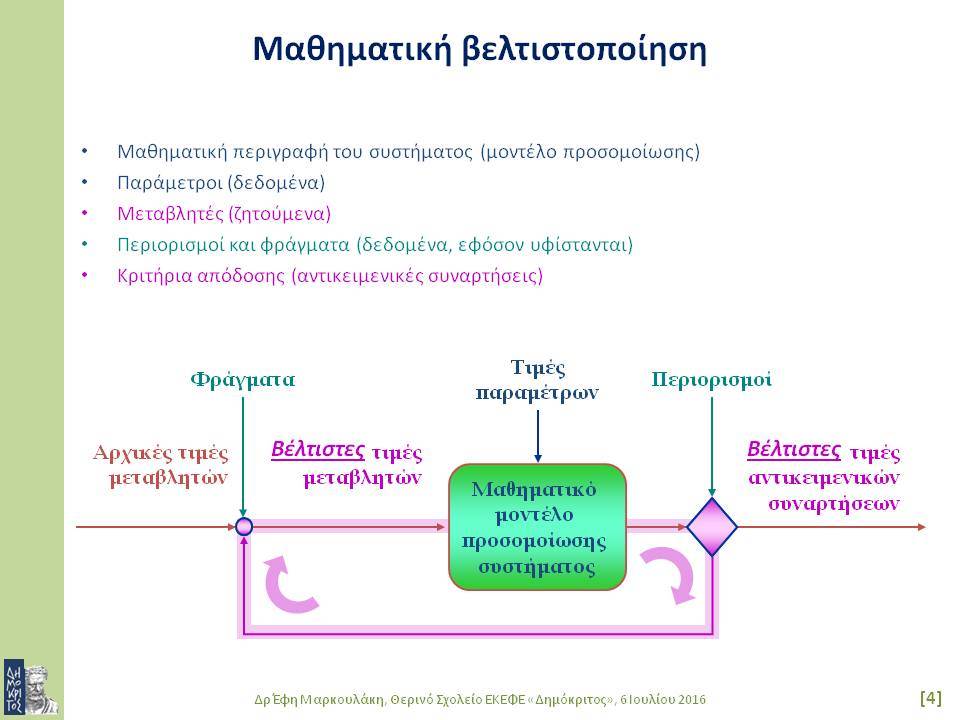
Πολλά προβλήματα μηχανικής βιομηχανικών διεργασιών απαιτούν τη συστηματική αναζήτηση μιας ή περισσότερων βέλτιστων λύσεων. Για παράδειγμα, η σύνθεση σχεδίων εξοπλισμού για τη βελτίωση υπαρχόντων διεργασιών ή την παραγωγή νέων προϊόντων ή ο σχεδιασμός καινοτόμων υλικών. Η αναζήτηση προϋποθέτει κριτήρια απόδοσης που να επιτρέπουν τη σύγκριση μεταξύ των εναλλακτικών λύσεων. Συνήθως, αυτά είναι κριτήρια οικονομικά ή/και περιβαλλοντικά, καθώς και η ενεργειακή κατανάλωση, η αξιοπιστία κ.ά. Τα προβλήματα αυτά έχουν πολλές μεταβλητές (π.χ. δυναμικότητα, τύπος εξοπλισμού) και περιορισμούς (π.χ. για ασφαλή λειτουργία) και περιλαμβάνουν την επίλυση δύσκολων (π.χ. μη-γραμμικών, ασυνεχών) εξισώσεων.
 

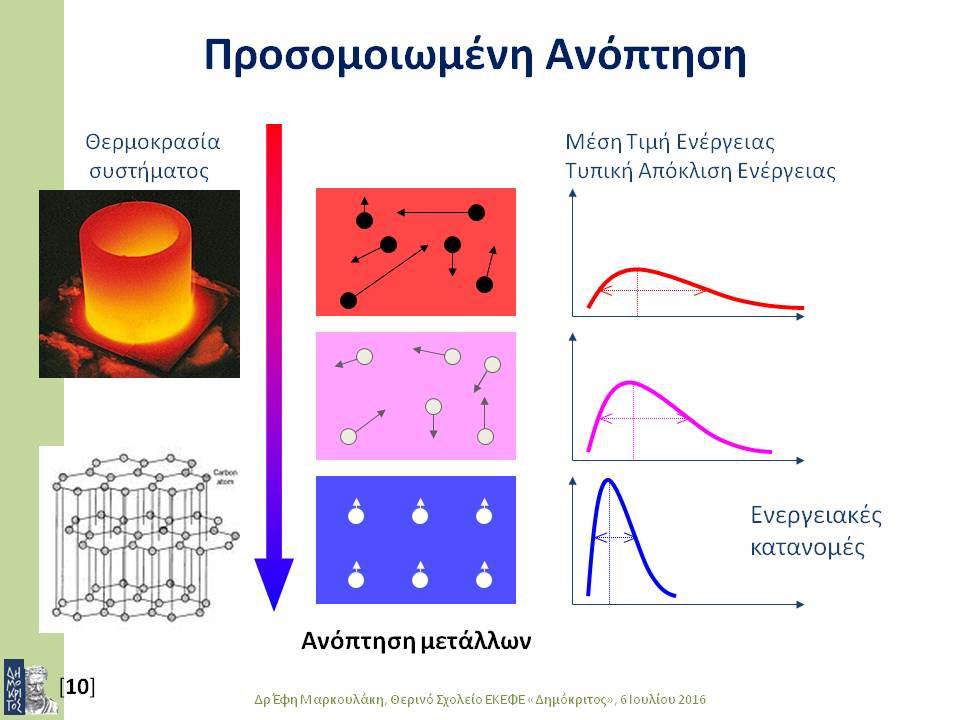
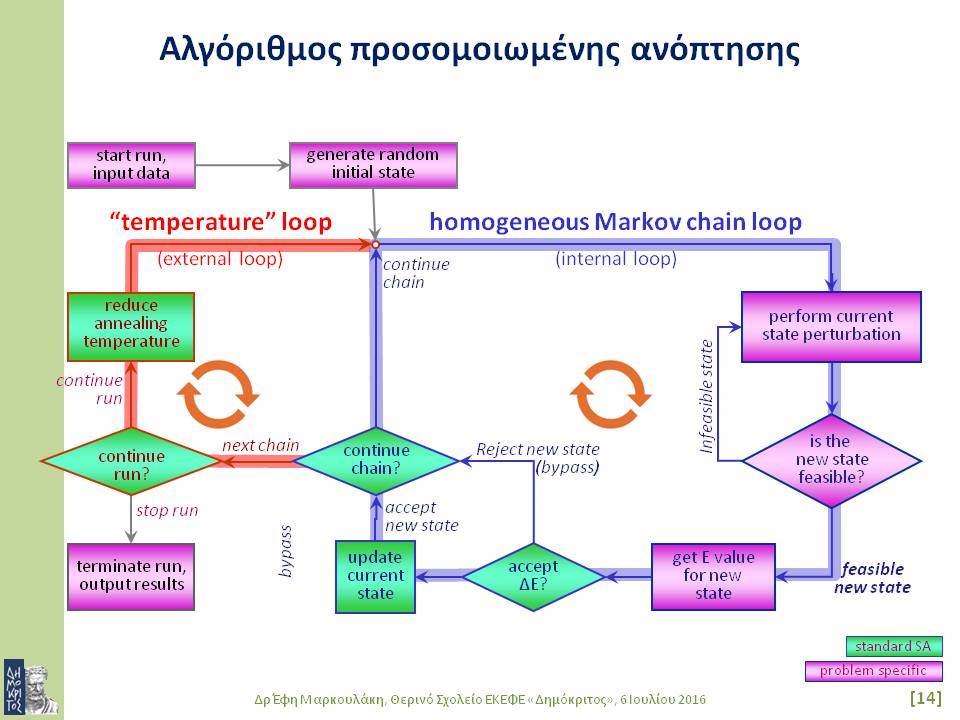
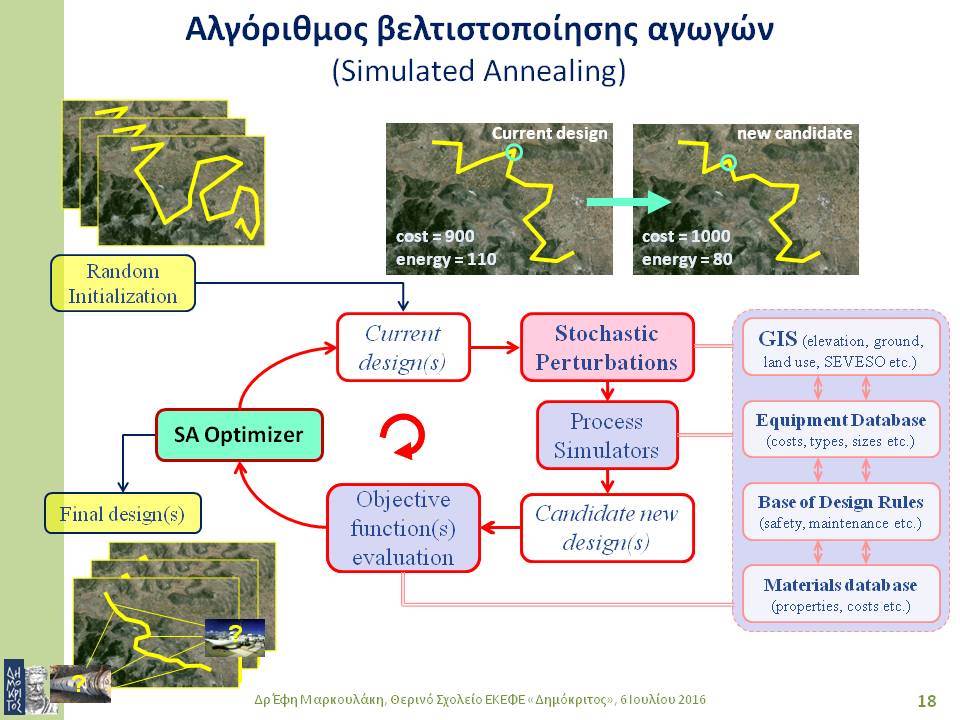
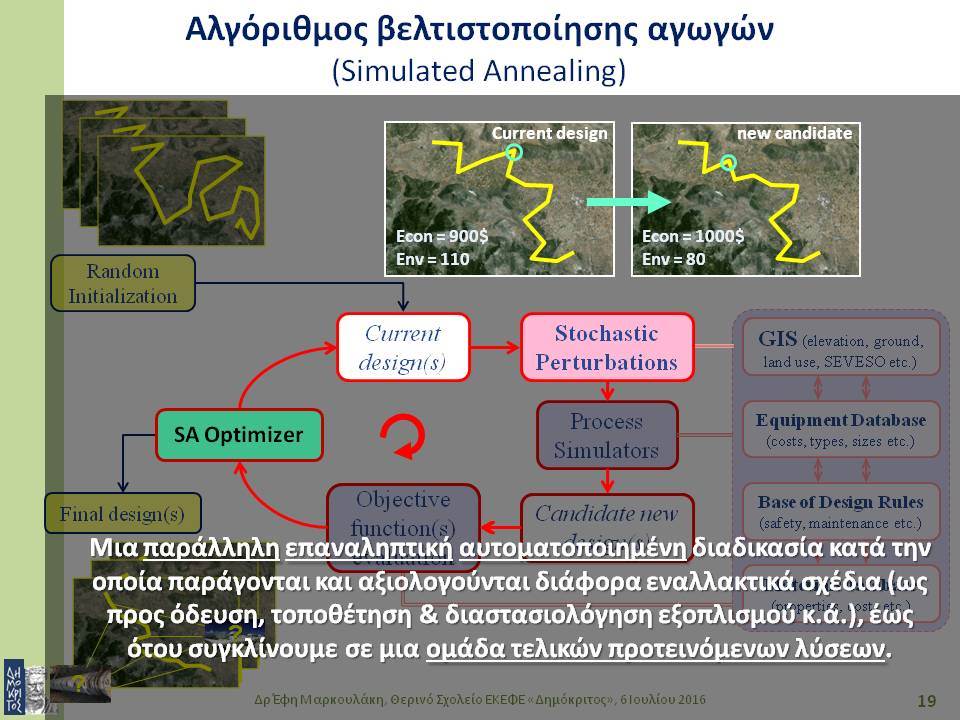
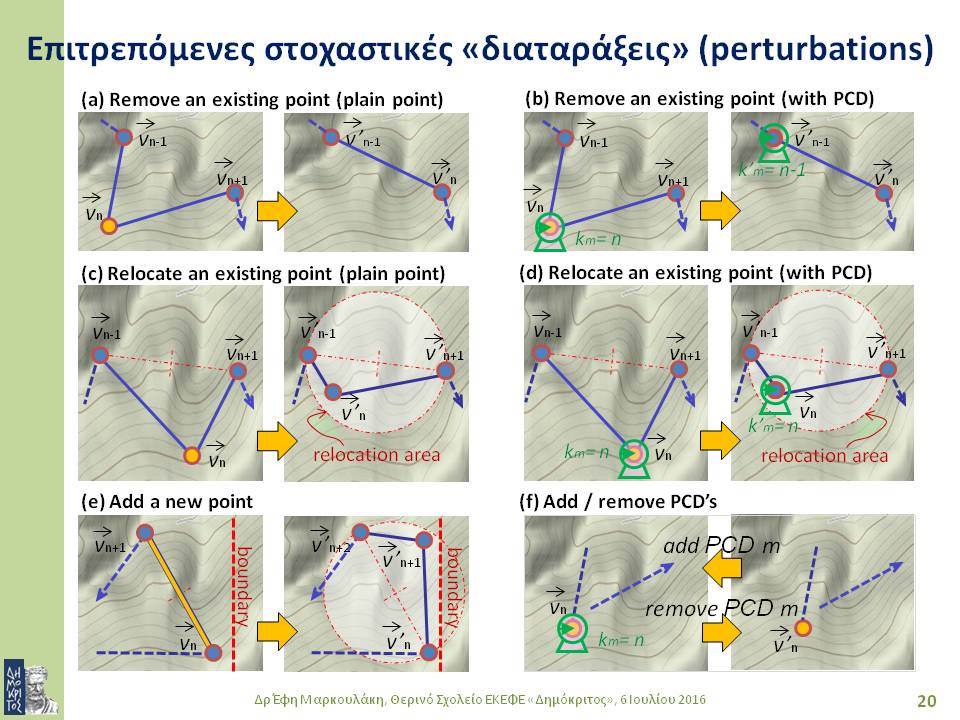
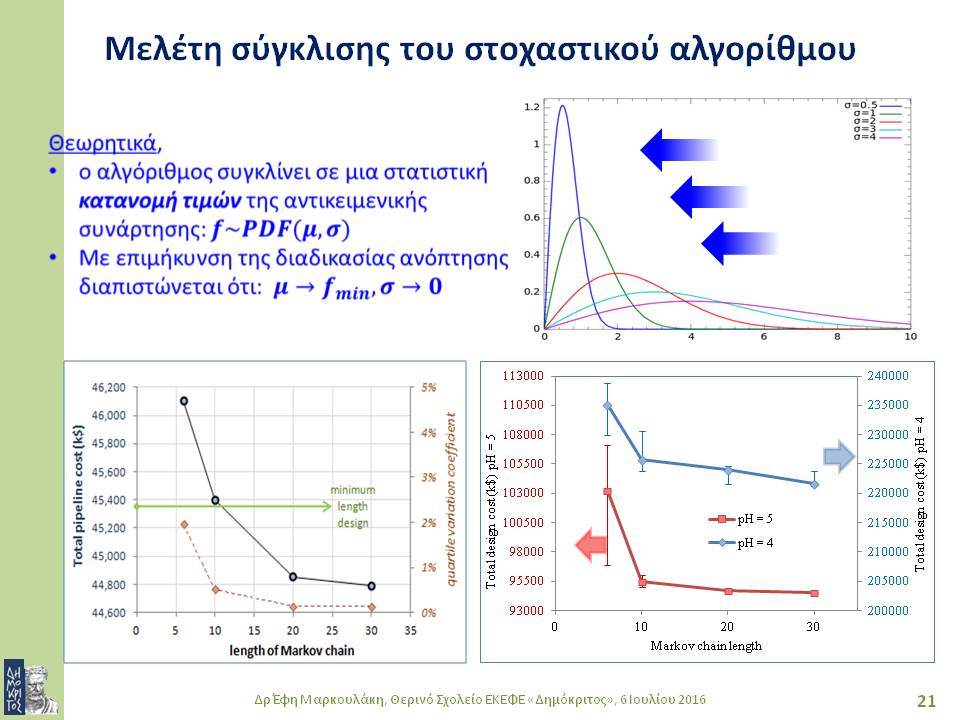
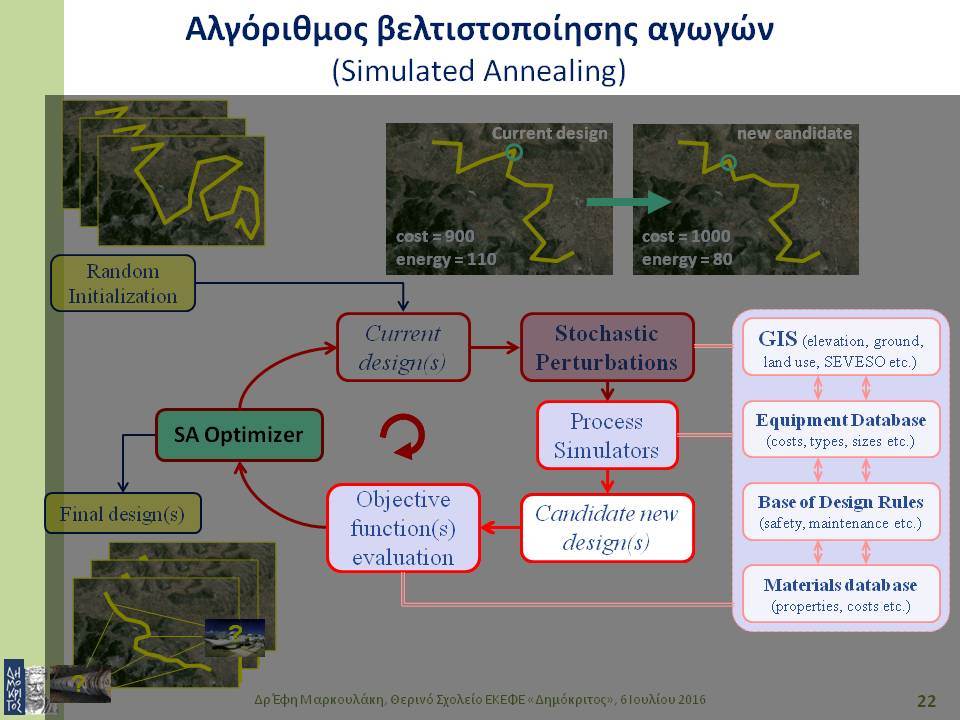
Στο πρώτο μέρος της διάλεξης θα γίνει μια σύντομη εισαγωγή στη μαθηματική βελτιστοποίηση και σε σημαντικές μεθόδους μαθηματικής βελτιστοποίησης. Στις μεθόδους αυτές συγκαταλέγονται ειδικοί αλγόριθμοι για τη συστηματική καθοδήγηση της διαδικασίας αναζήτησης βέλτιστων λύσεων προς υποσχόμενες περιοχές του πεδίου τιμών. Η στοχαστική αναζήτηση εφαρμόζει τυχαίες μεταβάσεις στο σύνολο των εναλλακτικών λύσεων, με πιθανότητές μετάβασης που ενισχύουν στατιστικά την προοδευτική προσέγγιση των περιοχών βέλτιστων λύσεων. Πολλοί αλγόριθμοι στοχαστικής βελτιστοποίησης υιοθετούν τεχνικές που βασίζονται σε φυσικούς ή βιολογικούς μηχανισμούς. Σε αυτή την κατηγορία αλγορίθμων ανήκουν η προσομοιωμένη ανόπτηση (simulated annealing), οι γενετικοί αλγόριθμοι (genetic algorithms), οι αλγόριθμοι ευφυίας σμήνους (swarm intelligence).

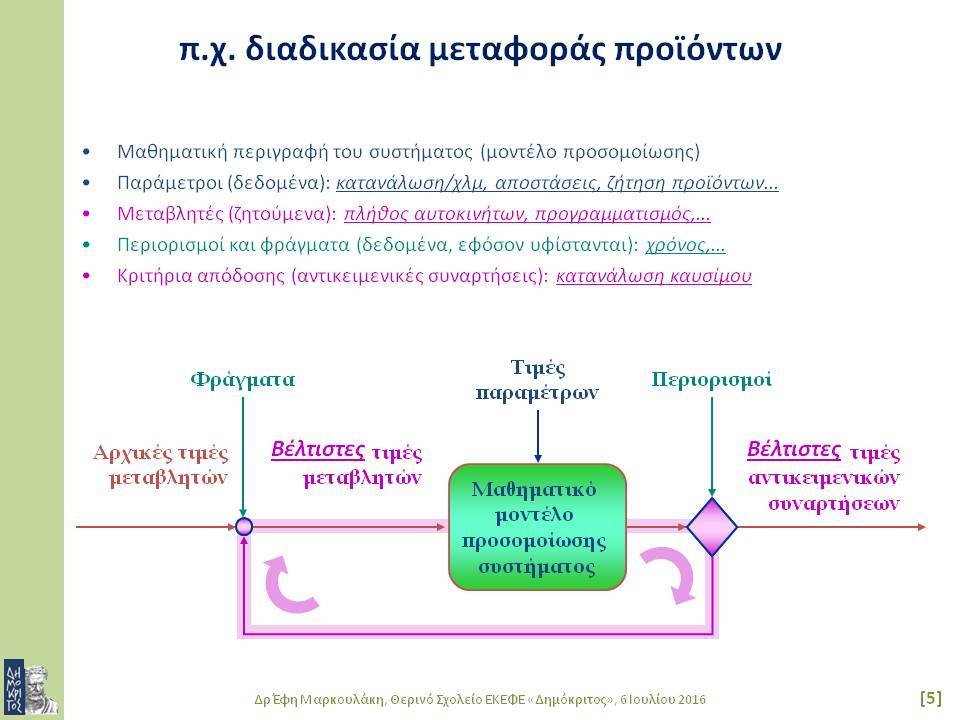
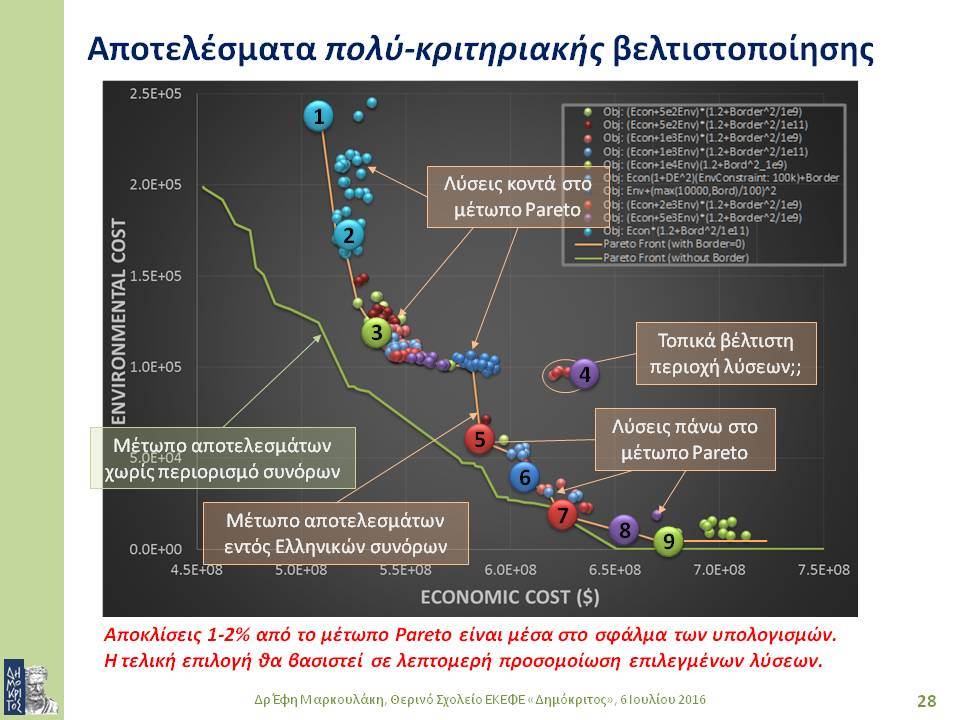
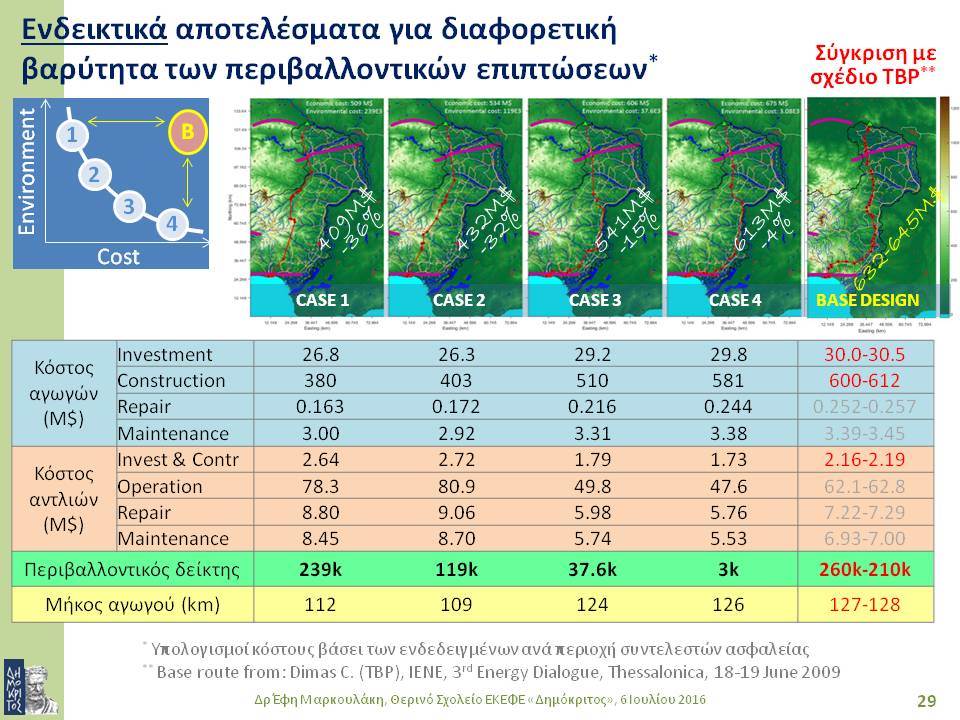
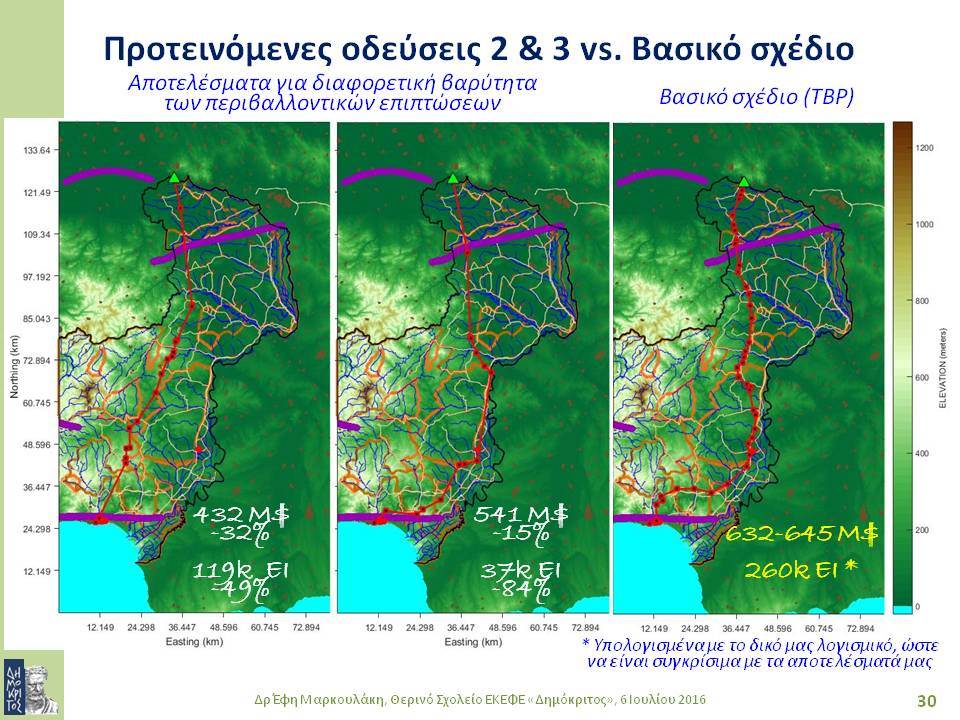
Οι στοχαστικές μέθοδοι βελτιστοποίησης ενδείκνυνται για συνδυαστικά συστήματα μεγάλης κλίμακας που έχουν πολλά ακρότατα, καθώς επίσης και για προβλήματα με περισσότερα του ενός κριτήρια απόδοσης. Το δεύτερο μέρος της διάλεξης εστιάζει στο βέλτιστο σχεδιασμό συστημάτων αγωγών για μεταφορά ρευστών, όπως είναι το πετρέλαιο, το φυσικό αέριο ή το νερό. Η ιδιαιτερότητα της συγκεκριμένης εφαρμογής έγκειται στο ότι ένα

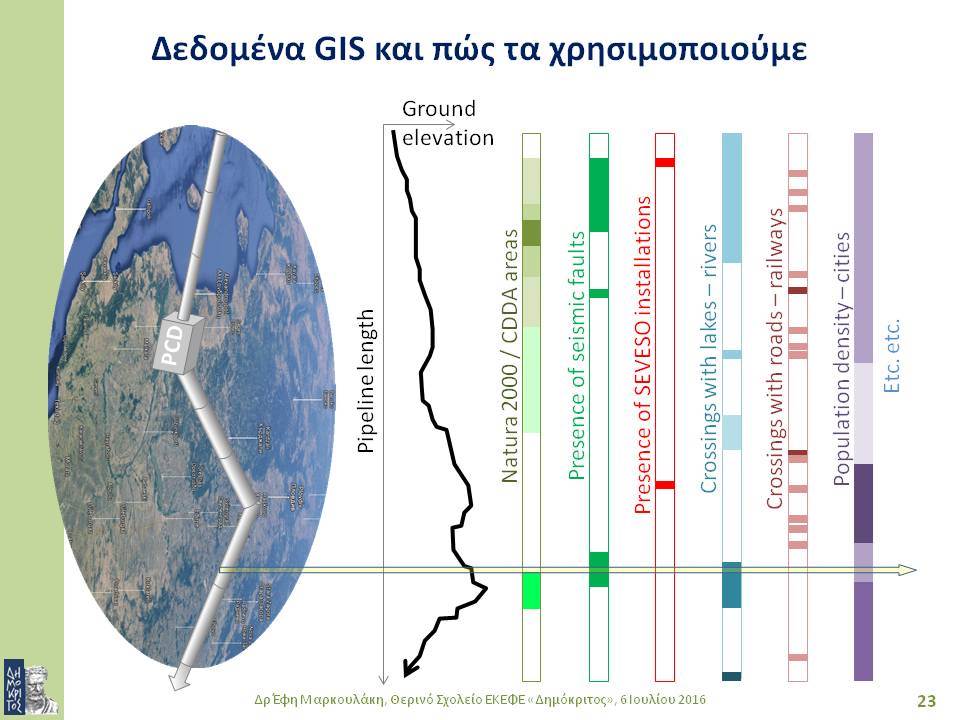
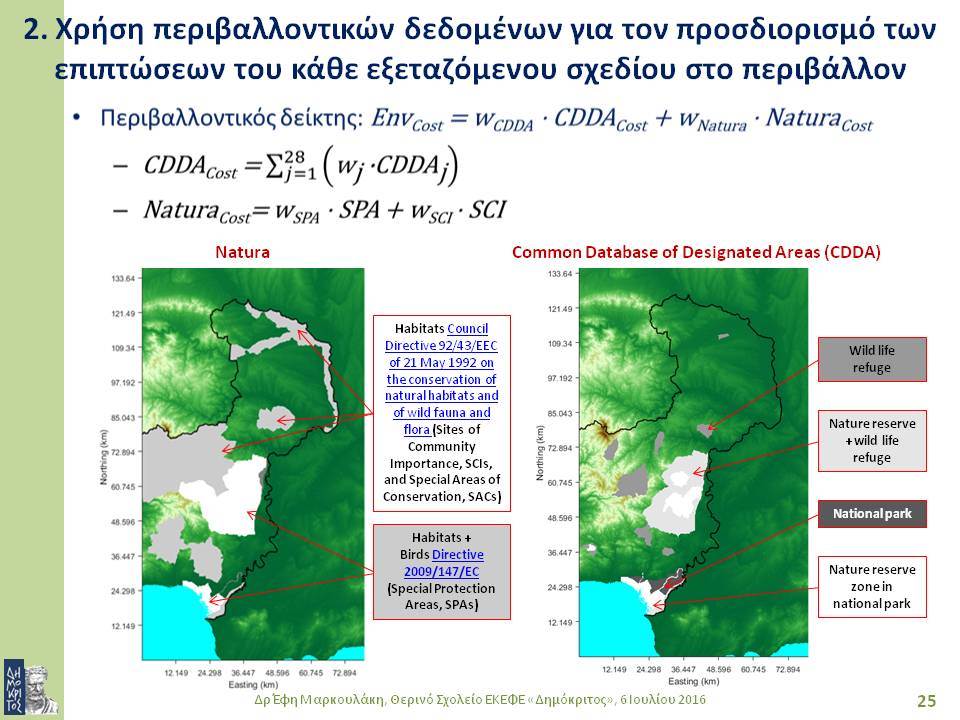
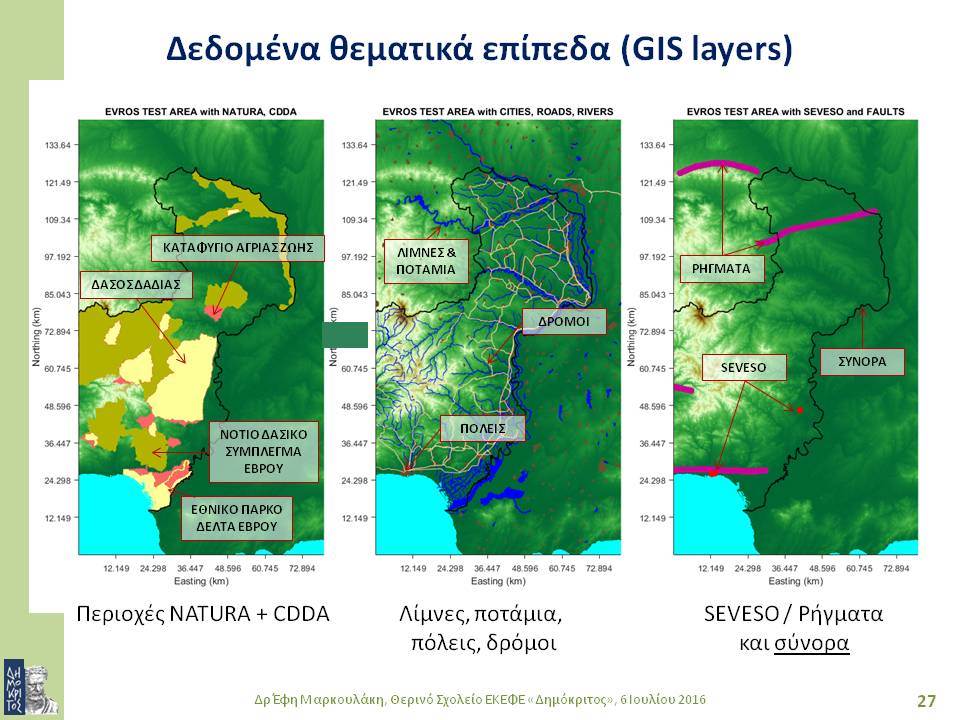
τέτοιο σύστημα εξαρτάται απόλυτα από τα γεωγραφικά χαρακτηριστικά της περιοχής από όπου διέρχεται: επηρεάζεται και την επηρεάζει. Επομένως, κατά το σχεδιασμό του συστήματος είναι απαραίτητο να ληφθούν υπόψη πλήθος γεωγραφικών δεδομένων από GIS. Τελειώνοντας, παρουσιάζονται αποτελέσματα από το σχεδιασμό ενός πραγματικού συστήματος, λαμβάνοντας υπόψη θέματα οικονομικά, περιβαλλοντικά και ασφάλειας.