



ΤΑΥΤΟΤΗΤΑ ΟΜΙΛΙΑΣ
Αλικάκος Νικόλαος
Γλώσσα
Ελληνική
Ημερομηνία
05/04/2023
Διάρκεια
00:25:57
Εκδήλωση
1η Διάλεξη του κύκλου "Οι εφαρμογές των Μαθηματικών στην σύγχρονη κοινωνία"
Χώρος
Ίδρυμα Ευγενίδου
Διοργάνωση
Ίδρυμα Ευγενίδου
Κατηγορία
Μαθηματικά
Ετικέτες
μαθηματικά, εφαρμογές των μαθηματικών, σύγχρονη κοινωνία, παραγοντοποίηση ακεραίων, κρυπτογραφία, τεχνικές κρυπτογράφησης, Επιστήμη των Υλικών, μαθηματική ανάλυση, επιδημία, πανδημία, COVID-19, μελέτη επιδημιών, προσομοίωση, μαθηματικά αιχμής, αλγόριθμοι, θεωρία παιγνίων
ΣΥΝΟΨΗ
Τα Μαθηματικά, που η σημερινή τους ηλικία ξεπερνάει τα 3.000 χρόνια, προσφέρουν την απόλυτη ανθρώπινη σκέψη και γλώσσα σε ό,τι αφορά στην αυστηρή ανθρώπινη επικοινωνία. Με την γλώσσα των Μαθηματικών μπορούμε να διαχειριζόμαστε αλλά και να ανταλλάσσουμε οσοδήποτε πολύπλοκες έννοιες και λογικά επιχειρήματα χωρίς κανένα απολύτως λάθος.
Με την πάροδο του χρόνου άρχισε να δημιουργείται μια διάκριση μεταξύ των επιστημόνων που παρήγαγαν νέα μαθηματική γνώση και αυτών που χρησιμοποιούσαν αυτήν την γνώση. Έτσι καταλήξαμε να μιλάμε για Θεωρητικά και για Εφαρμοσμένα Μαθηματικά. Όμως στη σύγχρονη εποχή, οι ανάγκες για μαθηματική σκέψη και τεχνικές διαχείρισης μεθόδων σχεδόν σε κάθε ανθρώπινη δραστηριότητα, η διάκριση μεταξύ θεωρίας και εφαρμογής έχει πλέον εξαφανιστεί. Και αυτό για τον απλό λόγο ότι δεν υπάρχουν πια μαθηματικές θεωρίες που δεν έχουν εφαρμογή σε κάποια ανθρώπινη δραστηριότητα. Αντίθετα, οι απαιτούμενες σήμερα μαθηματικές μέθοδοι όχι απλά δεν περισσεύουν αλλά λείπουν από το σύνολο των αναγκών μας.
Στόχος της παρούσας συνάντησης είναι να προβληθούν μερικές από τις σύγχρονες επιστημονικές και τεχνολογικές περιοχές όπου τα Μαθηματικά αποτέλεσαν και αποτελούν το άλφα και το ωμέγα της ύπαρξής τους.
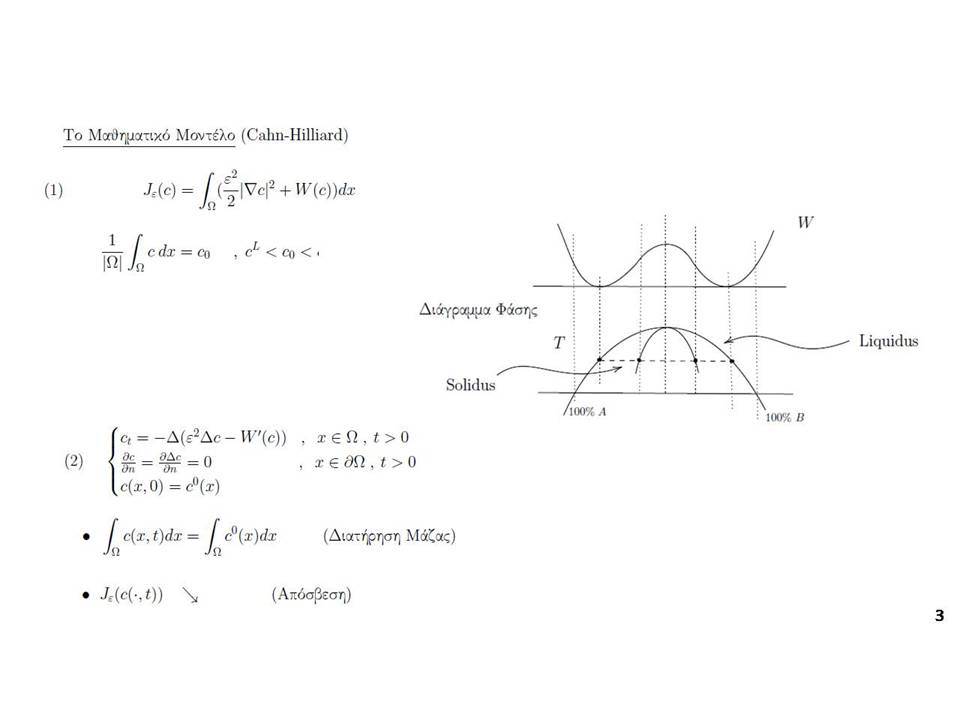
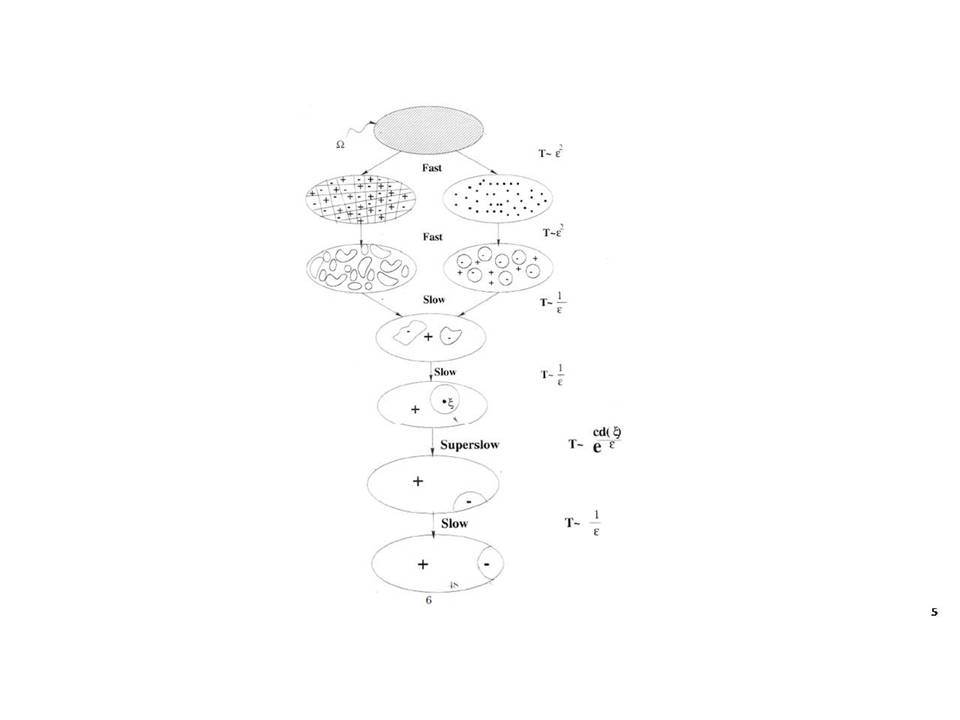
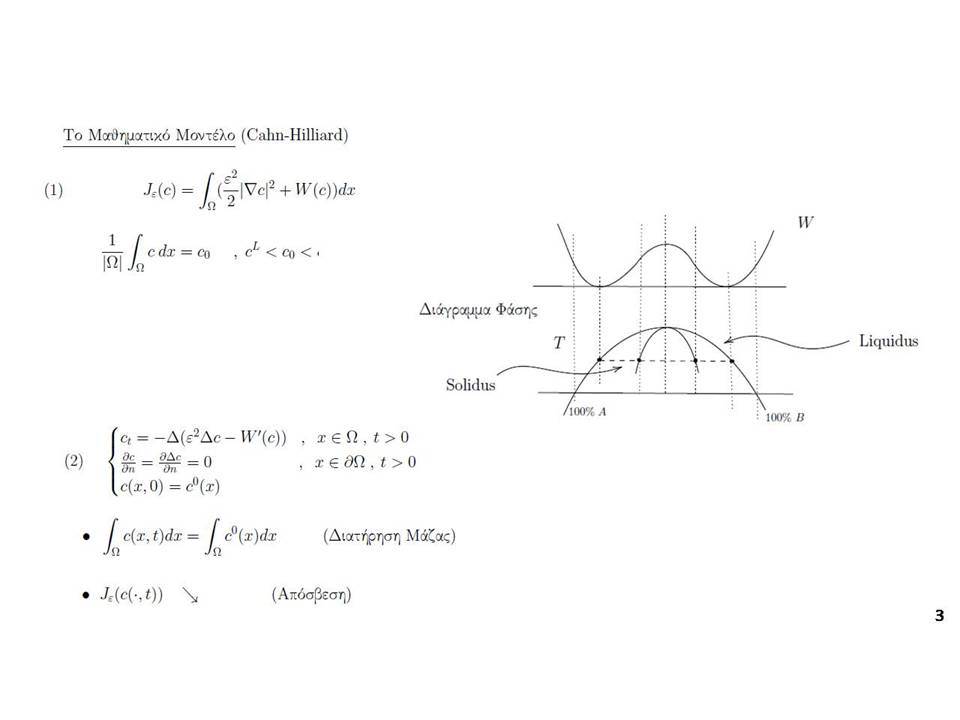
«Μαθηματική ανάλυση και Επιστήμη των Υλικών: Μερικά Παραδείγματα»
Αλικάκος Νικόλαος, Ομότιμος Καθηγητής Παν/μίου Αθηνών
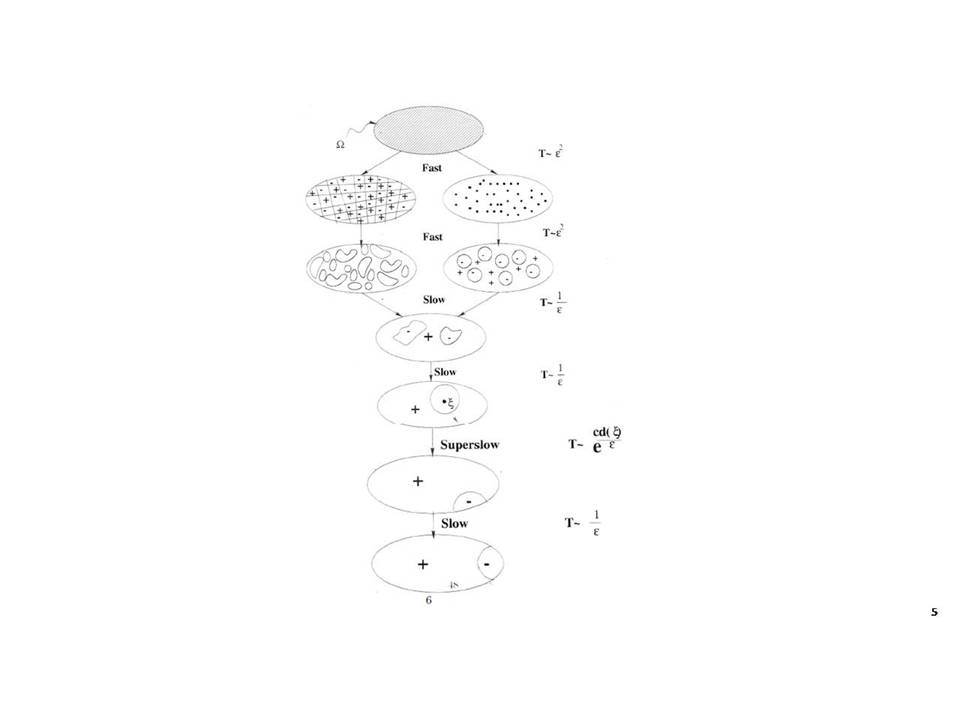
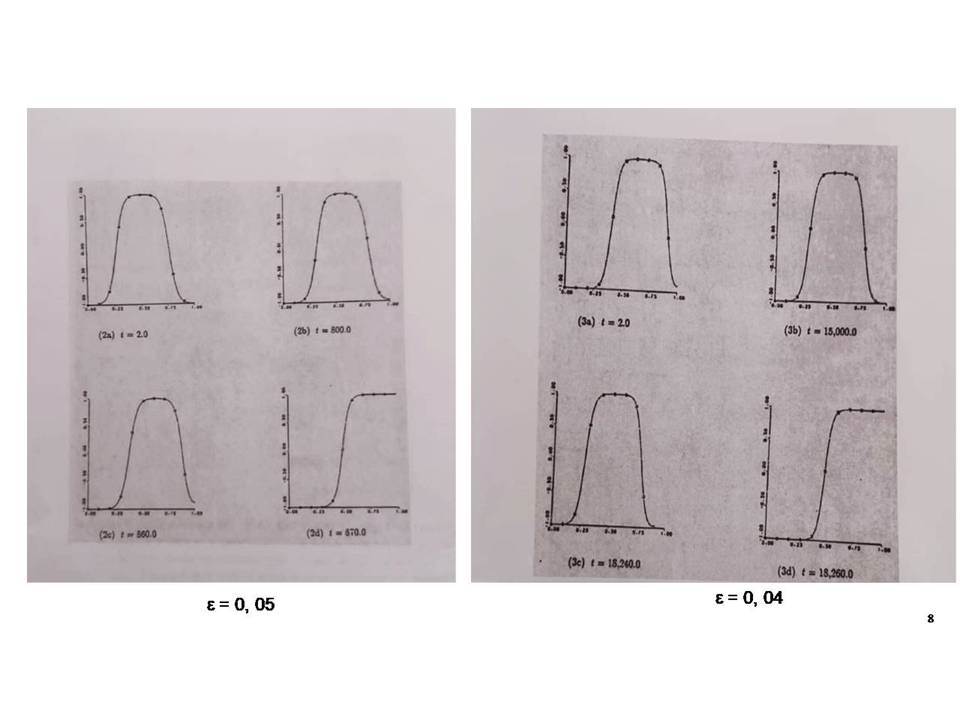
Τα πειράματα, και στην εποχή μας οι αριθμητικές προσομοιώσεις, είναι τα κύρια εργαλεία για την κατανόηση της φύσης.Όμως αυτές οι τόσο καθιερωμένες προσεγγίσεις, έχουν δύο μειονεκτήματα:Αφ’ ενός υπάρχουν φαινόμενα που είναι ιδιαίτερα δύσκολο να τα συλλάβουν τα πειράματα ή οι προσομοιώσεις, όπως προβλήματα στα οποία συνυπάρχουν πολλές διαφορετικές κλίμακες μεγάλης διαφοράς στις τάξεις μεγέθους.Αφετέρου, ακόμη και στις περιπτώσεις που ένα πρόβλημα μπορεί κανείς να το χειριστεί πειραματικά ή αριθμητικά, μπορεί να υπάρχει μια σοβαρή έλλειψη κατανόησης ‒εν γένει δεν ενδιαφέρει μόνον μια φαινομενολογική περιγραφή‒ αλλά και μια ικανοποιητική εξήγηση των μηχανισμών πίσω από την παρατήρηση.Αυτό είναι ακριβώς το σημείο όπου η πιο θεωρητική ανάλυση υπεισέρχεται: υπάρχουν πολλά μαθηματικά μοντέλα στις φυσικές επιστήμες όπου η αλληλοεπίδραση ενός μικρού αριθμού ποσοτήτων-παραμέτρων έχει ως αποτέλεσμα μια πληθώρα φαινομένων, συμπεριλαμβανομένων και αυτών που λόγω της συνύπαρξης πολλών κλιμάκων δεν είναι δυνατή η κατανόησή τους πειραματικά ή μέσω προσομοίωσης. Με την βοήθεια της Μαθηματικής Ανάλυσης, μπορεί κανείς πολλές φορές αυστηρά να εξηγήσει τις παρατηρήσεις με το να τις συσχετίσει με μερικές από τις παραμέτρους που χαρακτηρίζουν το μοντέλο, και με αυτό τον τρόπο να επιβεβαιώσει (ή να διαψεύσει) την εγκυρότητά του.Σε αυτήν την ομιλία θα δοθούν κάποια παραδείγματα τέτοιων φαινομένων όπου συνυπάρχουν πολλές κλίμακες, και που προέρχονται από την περιοχή της επιστήμης των υλικών, και θα παρουσιαστεί η προσφορά της Μαθηματικής Ανάλυσης στην κατανόησή τους.
ΟΜΙΛΗΤΕΣ
Γεννήθηκε στην Αθήνα το 1952. Τέλειωσε το Κολλέγιο Αθηνών το 1971, το University of Massachusetts (Amherst) το 1974 και το Brown University το 1978.
Εξελέγη Καθηγητής στο Πανεπιστήμιο Κρήτης το 1988, και Καθηγητής στο ΕΚΠΑ το 1993, στο γνωστικό αντικείμενο των Μερικών Διαφορικών Εξισώσεων.
Ήταν στο διδακτικό προσωπικό στο Purdue (Lafayette), στο University of Tennessee (Knoxville), και στο Πανεπιστήμιο του Texas (Denton). Ήταν Visiting Scholar στο Πανεπιστήμιο του Stanford το 2009 και το 2012, Professeur Invite στο Universite Pierre et Marie Curie (Paris6) το 2010 και στο Universite Paris-Sud (Orsay) το 2015, και επισκέπτης καθηγητής στο Courant Institute (New York University) για ακαδημαϊκά εξάμηνα το 2016, και το 2021.
Έχει δώσει Invited Address στην Αμερικανική Μαθηματική Εταιρεία, και ήταν Keynote Lecturer στο Equadiff στο Βερολίνο. Έχει βραβευτεί με ARISTEIA GRANT, και είναι Επιστημονικός Σύμβουλος στο Bulletin of the Hellenic Mathematical Society. Έχει επιβλέψει το Διδακτορικό των:
Ε. Στεφανόπουλος (Καθηγητής Παν. Πατρών), M. Kowlaczyk (Καθηγητής Παν. Χιλής), Γ. Κάραλη (Καθηγήτρια στο Παν. Κρήτης), Χ. Σουρδής (Ερευνητής στο Παν. Κρήτης), Ν. Κατζουράκης (Αναπληρωτής Καθηγητής στο Παν. του Reading), Π. Σμυρνέλης (Επίκουρος Καθηγητής στο ΕΚΠΑ), Α. Δαμιάλης (Διευθυντής Εκδόσεων το Journal of the European Mathematical Society), Π. Αντωνόπουλος (Καθηγητής Μέσης Εκπαίδευσης), Α. Φαλιάγκας (Υπουργείο Οικονομικών).
Έχει συγγράψει μία Μονογραφία, δύο διδακτικά βιβλία, και 85 επιστημονικά άρθρα. Το έργο του έχει 3946 citations, και ένα του άρθρο 648 citations (Google Scholar).